Реляційні бази даних

Лекція

5.1. Основні поняття

5.2. Операція вибірки (або обмеження)

5.3. Операція проекції

5.4. Операція декартового добутку

5.5. Операція об'єднання

5.6. Операція різниці

5.7. Операції з'єднання

5.8. Операція перетинання

5.9. Операція ділення

5.10. КОНТРОЛЬНІ ПИТАННЯ

Мета

Мета розділу – розглянути реляційну алгебру, як теоретичну мову операцій.

5.1. Основні поняття

Реляційна алгебра – це теоретична мова операцій, яка на основі одного або декількох відношень дозволяє створити інше відношення без зміни вихідних даних [1, 4, 6, 7, 9, 10, 12].

Обидва операнди й результат є відношеннями, а тому результати однієї операції можуть стати вихідними даними для іншої. Це дозволяє створювати вкладені вирази реляційної алгебри так само, як і арифметичні. Ця властивість називається замкнутістю, тобто відношення покриваються реляційною алгеброю так само, як числа арифметичними операціями [4].

Реляційна алгебра є мовою послідовного використання відношень, де усі кортежі, навіть узяті із різних відношень, обробляються однією командою без організації циклів. Для команд реляційної алгебри запропоновано кілька варіантів синтаксису. Далі ми скористаємося загальноприйнятими символічними позначеннями для цих команд і подамо їх у неформальному вигляді. Більш детально це питання для зацікавлених читачів розглянуто у роботах Ульмана (Ullman, 1988).

Існує декілька варіантів вибору операцій, які входять в реляційну алгебру. Спочатку Кодд запропонував вісім операторів, але згодом до них були додані ще деякі інші. П'ять основних операцій реляційної алгебри (рис. 5.1): вибірка (selection), проекція (projection), декартів добуток (cartesian product), об'єднання (union) і різниця (set difference) виконують більшість операцій витягу даних, які мають для нас інтерес. На базі п'яти основних операцій можна отримати додаткові (з'єднання (join), перетинання (intersection) і ділення (division) рис. 5.1).

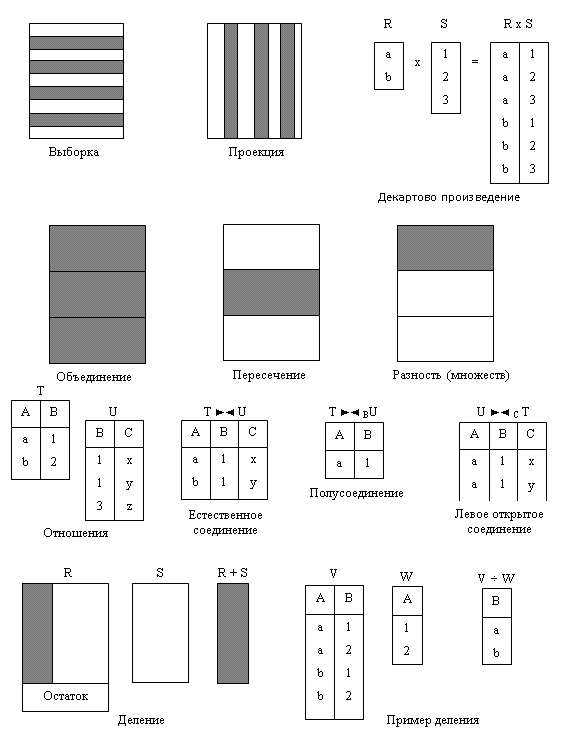
Рис. 5.1. Схематичне подання функцій операторів реляційної алгебри

Операції вибірки й проекції є унарними, оскільки вони працюють із одним відношенням. Інші операції працюють із парами відношень, і тому їх називають бінарними операціями. У наведених нижче формулюваннях R і S – це два відношення, які визначені на атрибутах A = (a₁, a₂, …, a_n) та B = (b₁, b₂, …, b_n) відповідно. Для ілюстрації результатів виконання операцій ми скористаємося відношеннями БД «БІБЛІОТЕКА» (додаток В).

5.2. Операція вибірки (або обмеження)

σ_{предикат}(R)

Операція вибірки працює з одним відношенням R і визначає результуюче відношення, яке містить тільки ті кортежі (рядка) відношення R, які задовольняють заданій умові (предикату).

ПРИКЛАД 5.1

Складіть список бібліотекарів, у яких табельний номер перевищує 80.

σ_ClockNumber > 80 (Librarians)

Тут вихідним є відношення Librarians, а предикатом – вираз ClockNumber>80. Операція вибірки визначає нове відношення, що містить тільки ті кортежі відношення Librarians, де значення атрибута ClockNumber перевищує 80 (табл. 5.1). Більш складні предикати можуть бути створені за допомогою логічних операторів AND, OR і NOT.

Таблиця 5.1

Результат виконання операції вибірки з відношення *Librarians*
Code	ClockNumber	FamilyName	Name	Patronymic	PasportCode	Post	HomePhone	Note
3	187	Іноземцева	Іванна	Модестівна	9	Ст. бібліотекар	775-XX-00	null
4	83	Мальцева	Діана	Петрівна	12	Бібліотекар	29-XX-15	null
6	100	Ставка	Лілія	Іванівна	7	Бібліотекар	22-XX-01	null

5.3. Операція проекції

П_{атр 1, …, атр n} (R)

Операція проекції працює з одним відношенням R і визначає нове, яке має вертикальну підмножину відношення R, що створено за допомогою витягу значень указаних атрибутів та виключення з результату рядків-дублікатів.

ПРИКЛАД 5.2

Складіть список бібліотекарів із зазначенням табельного номера (ClockNumber), прізвища (FamilyNamе), імені (Name), по батькові (Patronymic) та номера домашнього телефона (HomePhone).

П_{ClockNumber, FamilyName, Name, Patronymic, HomePhone} (R)

У цьому прикладі операція проекції визначає нове відношення, яке буде містити тільки атрибути ClockNumber, FamilyNamе, Name, Patronymic і HomePhone відношення Librarians, розміщені в зазначеному порядку (табл. 5.2).

Таблиця 5.2

Проекція відношення *Librarians*
ClockNumber	FamilyName	Name	Patronymic	HomePhone
28	Іванова	Олена	Володимирівна	52-XX-75
12	Ніколаєнко	Любов	Миколаївна	46-XX-19
187	Іноземцева	Іванна	Модестівна	775-XX-00
83	Мальцева	Діана	Петрівна	29-XX-15
10	Сизранцева	Тетяна	Ігорівна	370-XX-22
100	Ставка	Лілія	Іванівна	22-XX-01
50	Лещенко	Алла	Федорівна	722-XX-36
36	Сіра	Лідія	Іванівна	254-XX-02
45	Прохіна	Тамара	Львівна	63-XX-01
78	Самійленко	Вікторія	Ігорівна	125-XX-80
69	Степанова	Олександра	Миколаївна	445-XX-65
17	Петрова	Алина	Сергіївна	999-XX-05

5.4. Операція декартового добутку

R × S

Операція декартового добутку визначає нове відношення, яке є результатом конкатенації (зчеплення) кожного кортежу відношення R з кожним кортежем відношення S.

Операції вибірки та проекції дозволяють витягти інформацію тільки з одного відношення. Можливе виникнення і таких ситуацій, коли потрібна деяка комбінація даних з декількох відношень. Операція декартового добутку помножує два відношення. У результаті утворюється інше відношення, де є усі можливі пари кортежів обох відношень. Отже, якщо одне відношення має I кортежів та N атрибутів, а інше – J кортежів і M атрибутів, то відношення з їх декартовим добутком буде містити (I × J) кортежів та (N + M) атрибутів. Вихідні відношення можуть мати атрибути з однаковими іменами. У такому випадку імена атрибутів будуть містити назви відношень у вигляді префіксів. Це забезпечить унікальність імен атрибутів у результуючому відношенні.

ПРИКЛАД 5.3

Складіть список усіх читачів, які коли-небудь брали книжки у бібліотеці використовуючи такі атрибути відношення Readers: Code, FamilyName, Name та відношення BookGiveOutRecord: Code, ReaderCode, InventoryCode.

(П_{Code, FamilyName, Name} (Readers)) × (П_{Code, ReaderCode, InventoryCode}(BookGiveOutRecord))

Результатом виконання такої операції буде відношення, що містить 120 кортежів та 6 атрибутів. Наводити його у повному обсязі нема сенсу. Подивиться на його перші 12 кортежів (табл. 5.3). Перші 10 – усі можливі комбінації першого кортежу відношення Readers з десятьма кортежами відношення BookGiveOutRecord. Останні два наведені для того, щоб Ви порівняли їх значення з першими двома. Це перші дві можливі комбінації другого кортежу відношення Readers з першими двома кортежами відношення BookGiveOutRecord. Наступною буде третя можлива комбінація другого кортежу відношення Readers з третім кортежем відношення BookGiveOutRecord. І так до сто двадцятого кортежу.

Таблиця 5.3

Фрагмент декартового добутку відношень *Reader* і *BookGiveOutRecord*
Readers.Code	FamilyName	Name	BookGiveOutRecord.Code	ReaderCode	InventoryCode
1	Іванов	Петро	1	2	6
1	Іванов	Петро	2	3	4
1	Іванов	Петро	3	6	3
1	Іванов	Петро	4	4	6
1	Іванов	Петро	5	7	7
1	Іванов	Петро	6	9	12
1	Іванов	Петро	7	11	10
1	Іванов	Петро	8	7	8
1	Іванов	Петро	9	9	12
1	Іванов	Петро	10	12	15
2	Федорец	Ірина	1	2	6
2	Федорец	Ірина	2	3	4

У такому вигляді (120 кортежів) це відношення містить більше інформації, ніж це потрібно. Наприклад, перший кортеж цього відношення містить різні значення атрибутів Readers.Code і ReaderCode. Тому щоб одержати потрібний список (табл. 5.4), необхідно для цього відношення зробити операцію вибірки з витягом тільки тих кортежів, для яких виконується така умова: Readers.Code = ReaderCode. У цілому ця операція виглядає так:

σ_{Readers.Code = ReaderCode} (П_{Code, FamilyName, Name}(Readers)) × (П_{Code, ReaderCode, InventoryCode}(BookGiveOutRecord))

Таблиця 5.4

Обмежений декартів добуток відношень *Reader* і *BookGiveOutRecord*
Readers.Code	FamilyName	Name	BookGiveOutRecord.Code	ReaderCode	InventoryCode
2	Федорец	Ірина	1	2	6
3	Ільїн	Іван	2	3	4
6	Носенко	Олег	3	6	3
4	Суренко	Дмитро	4	4	6
7	Брусов	Володимир	5	7	7
9	Левченко	Юлія	6	9	12
11	Щиглів	Петро	7	11	10
7	Брусов	Володимир	8	7	8
9	Левченко	Юлія	9	9	12
12	Кириленко	Віктор	10	12	15

Як ми побачимо далі, комбінація операцій декартового добутку та вибірки може бути зведена до однієї операції – з'єднання

5.5. Операція об'єднання

R ∪ S

Операція об'єднання відношень R і S з кортежами I та J відбувається в результаті їх конкатенації з утворенням одного відношення з максимальною кількістю кортежів (I + J), якщо кортежі-дублікати виключені. При цьому відношення R і S мають бути сумісними за об'єднанням.

Об'єднання відношень можливо тільки у тому разі, коли збігаються їхні схеми, тобто коли вони мають однакову кількість атрибутів зі співпадаючими доменами (типами даних). Такі відношення є сумісними за об'єднанням. Відзначимо, що в деяких випадках для одержання двох сумісних за об'єднанням відношень може бути використана операція проекції.

ПРИКЛАД 5.4

Наведіть прізвища всіх користувачів, занесених в БД.

П_FamilyName(Readers) U П_FamilyName(Librarians)

Для створення сумісних за об'єднанням відношень спочатку слід застосувати операцію проекції, щоб виділити з відношень Readers і Librarians стовпці з атрибутами FamilyName, виключаючи у разі потреби дублікати. Потім для комбінування отриманих проміжних відношень слід використовувати операцію об'єднання (табл. 5.5).

Таблиця 5.5

Результат об'єднання відношень *Readers* і *Librarians* за атрибутом *FamilyName*
FamilyName
Брусов
Іванов
Іванова
Ільїн
Іноземцева
Кириленко
Козирєв
Коршунова
Левченко
Лещенко
Мальцева
Ніколаєнко
Носенко
Петрова
Прохіна
Сизранцева
Самійленко
Світла
Сіра
Ставка
Степанова
Суренко
Федорец
Щиглів

5.6. Операція різниці

R - S

Різниця двох відношень R і S складається з кортежів, які є у відношенні R, але відсутні у відношенні S. Причому відношення R й S мають бути сумісними за об'єднанням.

ПРИКЛАД 5.5

Визначіть індивідуальні коди читачів, які жодного разу не брали книжок у бібліотеці.

П_Code(Readers) – П_ReaderCode(BookGiveOutRecord)

У цьому випадку аналогічно попередньому прикладу слід створити сумісні за об'єднанням відношення Readers і BookGiveOutRecord, виконавши їх проекцію за атрибутами Code і ReaderCode. Далі слід використати операцію різниці (табл. 5.6).

Таблиця 5.6

Різниця відношень *Readers* і *BookGiveOutRecord* по атрибутам *Code* і *ReaderCode*
Code
1
5
8
10

5.7. Операції з'єднання

Як правило, користувачів цікавить лише деяка частина всіх комбінацій кортежів декартового добутку, яка задовольняє заданим умовам. Тому замість операції декартового добутку зазвичай використовується одна з найважливіших операцій реляційної алгебри – операція з'єднання. У результаті її виконання на базі двох вихідних відношень створюється нове. Операція з'єднання є похідною від операції декартового добутку. Вона еквівалентна операції вибірки з декартового добутку двох відношень тільки тих кортежів, які задовольняють умові, що наведена в предикаті з'єднання. Предикат з’єднання є еквівалентом. Реалізація операції з'єднання у реляційних СУБД – надскладне питання. У більшості випадків вона стає основною проблемою з підвищення продуктивності, що властива усім реляційним системам.

Розглянемо такі види операції з'єднання:

Тета-з'єднання (Θ-join).
З'єднання за еквівалентністю (equi-join) - окремий вид тета-з'єднання.
Натуральне з'єднання (natural join).
Зовнішнє з'єднання (outer join).
Напівз'єднання (semi-join).

5.7.1. Операція тета-з'єднання

R_►◄FS

Операція тета-з'єднання визначає відношення, яке містить кортежі з декартового добутку відношень R і S, що задовольняють предикату F. Предикат F має вигляд R.aiΘS.bi, де замість символу Θ може бути використаний один з операторів порівняння (<, <=,>, >=, =, ≈).

Операцію тета-з'єднання з урахуванням базових операцій вибірки й декартового добутку можна записати так:

R_►◄FS = σ_F(R × S).

Як і у разі з операцією декартового добутку, степенем тета-з'єднання називається сума степеней операндів-відношень R і S. Якщо предикат F містить тільки оператор рівності (=), то це – з'єднання за еквівалентністю.

ПРИКЛАД 5.6

Створіть список читачів, які коли-небудь брали книжки у бібліотеці (табл. 5.4).

У прикладі 5.3, щоб одержати цей список, використовують операції декартового добутку й вибірки. Однак такий самий результат можна одержати за допомогою операції з'єднання за еквівалентністю.

(П_{Code, FamilyName, Name}(Readers))_{►◄Readers.Code = ReaderCode}(П_{Code, ReaderCode, InventoryCode}(BookGiveOutRecord))

5.7.2. Операція натурального з'єднання

R_►◄S

З'єднання за еквівалентністю двох відношень R і S називається натуральним, якщо воно виконане за всіма спільними атрибутами x і з результатів виключено по одному екземпляру кожного спільного атрибута.

Степенем натурального з'єднання є сума степеней операндів-відношень R і S при відніманні кількості спільних атрибутів x. У прикладі з операцією тета-з'єднання для складання цього списку використовувалася операція з'єднання за еквівалентністю. У ньому були присутні два атрибути Readers.Code і ReaderCode, що містять коди читачів бібліотеки. Коли б вони мали однакове ім'я, наприклад ReaderCode, то для усунення одного з них можна скористатися операцією натурального з'єднання.

ПРИКЛАД 5.7

Створіть список читачів, які коли-небудь брали книжки в бібліотеці (табл. 5.7).

(П_{ReaderCode, FamilyName, Name}(Readers))_►◄(П_{Code, ReaderCode, InventoryCode}(BookGiveOutRecord))

Таблиця 5.7

Натуральне з'єднання відношень *Readers* і *BookGiveOutRecord* за атрибутом *ReaderCode*
ReaderCode	FamilyName	Name	BookGiveOutRecord.Code	InventoryCode
2	Федорец	Ірина	1	6
3	Ільїн	Іван	2	4
6	Носенко	Олег	3	3
4	Суренко	Дмитро	4	6
7	Брусов	Володимир	5	7
9	Левченко	Юлія	6	12
11	Щиглів	Петро	7	10
7	Брусов	Володимир	8	8
9	Левченко	Юлія	9	12
12	Кириленко	Віктор	10	15

5.7.3. Операція зовнішнього з'єднання

Найчастіше при з'єднанні двох відношень кортеж з одного відношення не знаходить відповідного кортежу в іншому відношенні. Інакше кажучи, в атрибутах, за якими відбувається операція з'єднання, виявляються незбіжні значення. Може знадобитися, щоб кортеж з одного або двох відношень був поданий у результаті з'єднання, навіть якщо у відповідних атрибутах немає співпадаючих значень. Ця мета може бути досягнута за допомогою операції зовнішнього з'єднання.

Відсутні значення у результуючому відношенні позначаються за допомогою визначника NULL. Перевагою операції зовнішнього з'єднання є зберігання вихідної інформації: кортежі, які втрачаються при використанні інших типів з'єднань.

R_⊃◄S

Лівим зовнішнім з'єднанням називається операція, коли кортежі відношення R, які не мають співпадаючих значень у спільних стовпцях з відношенням S, також включаються в результуюче відношення.

ПРИКЛАД 5.8

Визначить індивідуальні коди читачів, їх прізвища, ім’я, по батькові та інформацію про книжки, які вони брали у бібліотеці (табл. 5.8).

(П_{Code, FamilyName, Name, Patronymic}(Readers))_⊃◄(П_{OutLibrarianCode, InventoryCode, IssueDate, ReturnDate, FactReturnDate, InLibrarianCode}(BookGiveOutRecord))

Точно кажучи, у прикладі розглянута операція лівого (натурального) зовнішнього з'єднання, оскільки в результуючому відношенні присутні всі кортежі лівого відношення. Існує також праве зовнішнє з'єднання, назване так тому, що в результуючому відношенні присутні всі кортежі правого відношення. Крім того, існує й повне зовнішнє з'єднання, у результуючому відношенні якого містяться всі кортежі обох відношень, де для позначення незбіжних значень кортежів використовується визначник NULL.

Таблиця 5.8

Ліве зовнішне з'єднання проекцій відношень *Readers* та *BookGiveOutRecord*
ReaderCode	FamilyName	Name	Patronymic	OutLibrarianCode	InventoryCode	IssueDate	ReturnDate	FactReturnDate	InLibrarianCode
1	Іванов	Петро	Іванович	NULL	NULL	NULL	NULL	NULL	NULL
2	Федорец	Ірина	Олегівна	4	6	11.09.2004	25.09.2004	24.09.2004	3
3	Ільїн	Іван	Петрович	4	4	02.09.2004	16.09.2004	11.12.2004	3
4	Суренко	Дмитро	Павлович	3	6	30.10.2004	13.11.2004	10.01.2005	6
5	Коршунова	Наталя	Юріївна	NULL	NULL	NULL	NULL	NULL	NULL
6	Носенко	Олег	Володимирович	4	3	02.09.2004	16.09.2004	16.09.2004	1
7	Брусов	Володимир	Михайлович	9	8	07.03.2009	21.03.2009	10.04.2009	10
7	Брусов	Володимир	Михайлович	10	7	10.11.2009	24.11.2009	24.11.2009	12
8	Козирєв	Олексій	Сергійович	NULL	NULL	NULL	NULL	NULL	NULL
9	Левченко	Юлія	Павлівна	7	12	15.12.2009	29.12.2009	NULL	9
9	Левченко	Юлія	Павлівна	8	12	05.02.2010	29.02.2010	NULL	11
10	Світла	Тетяна	Іванівна	NULL	NULL	NULL	NULL	NULL	NULL
11	Щиглів	Петро	Євгенович	8	10	06.02.2009	20.02.2009	19.02.2009	7
12	Кириленко	Віктор	Олександрович	10	15	21.09.2010	05.10.2010	03.10.2010	9

5.7.4. Операція напівз’єднання

R_►FS

Операція напівз'єднання визначає відношення, яке містить ті кортежі відношення R, які входять у з'єднання відношень R і S.

Перевага операції напівз'єднання полягає в тому, що вона дозволяє зменшити число кортежів, які потрібно обробити для одержання з'єднання. Це особливо важливо при обчисленні з'єднань у розподілених системах. Операцію напівз'єднання можна сформулювати й за допомогою операторів проекції й з'єднання:

R_►FS = П_A(R_►◄FS)

Тут A – набір усіх атрибутів у відношенні R. Насправді, це напівтета-з'єднання, причому слід зазначити, що існують напівз'єднання за еквівалентністю та напівнатуральне з'єднання.

ПРИКЛАД 5.9

Створіть повний звіт, про всіх читачів на ім'я «Дмитро», які коли-небудь брали книжки в бібліотеці (табл. 5.9).

Readers_{►Readers.Code = BookGiveOutRecord.ReaderCode AND Reader.Name = ‘Дмитрий’}BookGiveOutRecord

Таблиця 5.9

Результат напівз'єднання відношень *Readers* і *BookGiveOutRecord*
Code	FamilyName	Name	Patronymic	ReaderCardNumber	PasportCode	Job	Post	Note
4	Суренко	Дмитро	Павлович	543	6	ДГУ, каф. геофізики	Ст. викладач	NULL

5.8. Операція перетинання

R ∩ S

Операція перетинання визначає відношення, яке містить кортежі, які є, як у відношенні R, так і у відношенні S. Відношення R й S мають бути сумісними за об'єднанням.

Операцію перетинання можна записати, використовуючи операції різниці між відношеннями: R ∩ S= R – (R – S).

ПРИКЛАД 5.10

Створіть список бібліотекарів, які є одночасно читачами. Укажіть їх код паспорта, прізвище, ім’я та по батькові.

(П_{PasportCode, FamilyName, Name, Patronymic}(Readers)) ∩ (П_{PasportCode, FamilyName, Name, Patronymic}(Librarians))

Для виконання умови сумісності відношень за об’єднанням були виконані відповідні операції проекції.

Дані, які входять до відношень «ЧИТАЧИ» та «БІБЛІОТЕКАРІ» (дод. В) свідчать, що результатом їх перетинання є порожня множина, тобто жоден з бібліотекарів не є читачем.

5.9. Операція ділення

Операція ділення може бути корисною у запитах особливого типу, які досить часто виконуються до БД. Припустимо, що відношення R визначене на множині атрибутів A, а відношення S – на множені атрибутів B, причому B ⊆ A (тобто B є підмножиною A). Нехай C =A - B, тобто C є множиною атрибутів відношення R, яка не є атрибутами відношення S. Тоді визначення операциъ ділення буде таким:

R ÷ S

Результатом операції ділення є набір кортежів відношення R, визначених на множині атрибутів C, які відповідають комбінаціям усіх кортежів відношення S.

Операція ділення еквівалентна низці інших основних операцій:

T₁ = П_C(R)

T₂ = П_C((S × T₁) – R)

T = T₁ – T₂

ПРИКЛАД 5.11

Створіть список імен, прізвищ, по батькові та кодів паспортів читачів, які народилися після 1 грудня 1960 року.

R = П_{Code, PassportCode, FamilyName, Name, Patronymic}(Readers) (табл. 5.10);

S = П_Code(σ_{Birthday > 31.12.1960}(PasportData)) (табл. 5.11);

R ÷ S = (П_{Code, PassportCode, FamilyName, Name, Patronymic}(Readers)) ÷ (П_Code(σ_{Birthday > 31.12.1960}(PasportData))) (табл. 5.12).

Для вирішенню поставленого завдання спочатку необхідно отримати відношення R. Для цього виконана проекція відношення Readers (табл. 5.10). Потім визначити відношення S. Для цього зроблена проекція відношення PasportData. У ньому за допомогою оператора вибірки знайдені всі коди паспортів з датою народження після 31 грудня 1960 року (табл. 5.11). Тепер отримаємо результат ділення відношення R на S (табл. 5.12).

Таблиця 5.10

Відношення R
Code	PasportCode	FamilyName	Name	Patronymic
1	4	Іванов	Петро	Іванович
2	1	Федорец	Ірина	Олегівна
3	11	Ільїн	Іван	Петрович
4	6	Суренко	Дмитро	Павлович
5	8	Коршунова	Наталя	Юріївна
6	5	Носенко	Олег	Володимирович
7	24	Брусов	Володимир	Михайлович
8	15	Козирєв	Олексій	Сергійович
9	18	Левченко	Юлія	Павлівна
10	22	Світла	Тетяна	Іванівна
11	14	Щиглів	Петро	Євгенович
12	17	Кириленко	Віктор	Олександрович

Таблиця 5.11

Відношення S
Code
3
5
7
8
12
14
15
16
18
19
20
21
22
23
24

Таблиця 5.12

Результат *R ÷ S*
PasportCode	FamilyName	Name	Patronymic
8	Коршунова	Наталя	Юріївна
5	Носенко	Олег	Володимирович
24	Брусов	Володимир	Михайлович
15	Козирєв	Олексій	Сергійович
18	Левченко	Юлія	Павлівна
22	Світла	Тетяна	Іванівна
14	Щиглів	Петро	Євгенович

5.10. КОНТРОЛЬНІ ПИТАННЯ

Які особливості та властивості реляційної алгебри Вам відомі?
Які операції реляційної алгебри Ви знаєте?
Яка існує різниця між операціями вибірки та проекції?
В якому із двох відношень кількість атрибутів та кортежів буде більшою, якщо перше є результатом операції декартового добутку відношень R з I кортежів та N атрибутів та S з J кортежів і M атрибутів, а друге – результатом операції об’єднання тих самих відношень?
У чому полягає сутність операцій реляційної алгебри, які потребують сумісних за об’єднанням вихідних відношень?
Які операції реляційної алгебри є похідними від операції декартового добутку?
Який з операторів порівняння перетворює Θ-з’єднання у натуральне?
У чому полягає різниця між зовнішнім та іншими типами з’єднань?
В чем разница между внешним и другими типами соединений?
Як формується відношення, що є результатом роботи відомих Вам типів зовнішніх з’єднань?

Висновок

Синтаксис SQL-операторів, які використовуються для обробки даних у реляційних СКБД різних розробників, може дещо відрізнятися, але операції реляційної алгебри є математичним фундаментом, що їх об'єднує. У разі необхідності цей факт може бути корисним для конвертації БД з реляційної СКБД, що використовується для розв’язання поточної задачі організації, у формат реляційної СКБД іншого розробника.

5. Реляційна алгебра

5.1. Основні поняття

5.2. Операція вибірки (або обмеження)

5.3. Операція проекції

5.4. Операція декартового добутку

5.5. Операція об'єднання

5.6. Операція різниці

5.7. Операції з'єднання

5.7.1. Операція тета-з'єднання

5.7.2. Операція натурального з'єднання

5.7.3. Операція зовнішнього з'єднання

5.7.4. Операція напівз’єднання

5.8. Операція перетинання

5.9. Операція ділення

5.10. КОНТРОЛЬНІ ПИТАННЯ