Цель
Цель раздела – рассмотрение реляционной алгебры, как теоретического языка операций
Реляционная алгебра – это теоретический язык операций, который на основе одного или нескольких отношений позволяет создавать другое отношение без изменения исходных данных [1, 4, 6, 7, 9, 10, 12].
Оба операнда и результат являются отношениями, а потому результаты одной операции могут стать исходными данными для другой. Это позволяет создавать вложенные выражения реляционной алгебры точно так же, как арифметические. Это свойство называется замкнутостью, т.е. отношения покрываются реляционной алгеброй так же, как числа арифметическими операциями [4].
Реляционная алгебра является языком последовательного использования отношений, в котором все кортежи, взятые даже из разных отношений, обрабатываются одной командой без организации циклов. Для команд реляционной алгебры предложено несколько вариантов синтаксиса. Далее мы воспользуемся общепринятыми символическими обозначениями для этих команд и представим их в неформальном виде. Более детально этот вопрос для заинтересованных читателей рассмотрен в работах Ульмана (Ullman, 1988).
Существует несколько вариантов выбора операций, которые включаются в реляционную алгебру. Сначала Кодд предложил восемь операторов, но впоследствии к ним были добавлены и некоторые другие. Пять основных операций реляционной алгебры, а именно выборка (selection), проекция (projection), декартово произведение (cartesian product), объединение (union) и разность (set difference), выполняют большинство операций извлечения данных, которые могут представлять для нас интерес. На основании пяти основных операций можно получить дополнительные (соединения (join), пересечения (intersection) и деления (division) рис. 5.1).
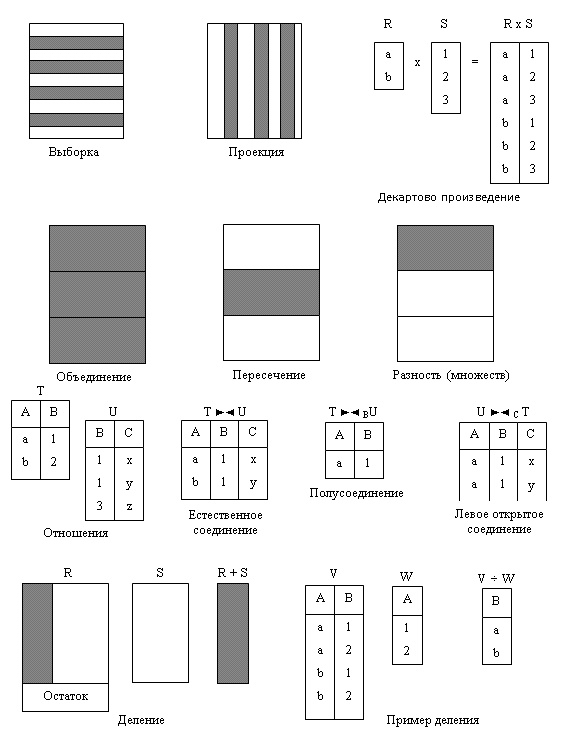
Рис. 5.1. Схематическое представление функций операторов реляционной алгебры
Операции выборки и проекции являются унарными, поскольку они работают с одним отношением. Другие операции работают с парами отношений, и поэтому их называют бинарными операциями. В приведенных ниже определениях R и S – это два отношения, определенные над атрибутами A = (a1, a2, …, an) и B = (b1, b2, …, bn) соответственно. Для иллюстрации результатов выполнения операций мы воспользуемся отношениями БД «БИБЛИОТЕКА» (приложение В).
5.2. Операция выборки (или ограничения)
| σпредикат(R) | Операция выборки работает с одним отношением R и определяет результирующее отношение, которое содержит только те кортежи (строки) отношения R, которые удовлетворяют заданному условию (предикату). |
ПРИМЕР 5.1
Составьте список библиотекарей, у которых табельный номер превышает 80.
σClockNumber > 80 (Librarians)
Здесь исходным отношением является отношение Librarians, а предикатом – выражение ClockNumber>80. Операция выборки определяет новое отношение, содержащее только те кортежи отношения Librarians, в которых значение атрибута ClockNumber превышает 80 (табл. 5.1). Более сложные предикаты могут быть созданы с помощью логических операторов AND, OR и NOT.
Таблица 5.1
Результат выполнения операции выборки из отношения Librarians | Code | ClockNumber | FamilyName | Name | Patronymic | PasportCode | Post | HomePhone | Note |
| 3 | 187 | Иноземцева | Иванна | Модестовна | 9 | Ст. библиотекарь | 775-XX-00 | null |
| 4 | 83 | Мальцева | Диана | Петровна | 12 | Библиотекарь | 29-XX-15 | null |
| 6 | 100 | Ставка | Лилия | Ивановна | 7 | Библиотекарь | 22-XX-01 | null |
5.3. Операция проекции
| Патр 1, …, атр n (R) | Операция проекции работает с одним отношением R и определяет новое отношение, содержащее вертикальное подмножество отношения R, создаваемое посредством извлечения значений указанных атрибутов и исключения из результата строк-дубликатов. |
ПРИМЕР 5.2
Составьте список библиотекарей с указанием табельного номера (ClockNumber), фамилии (FamilyNamе), имени (Name), отчества (Patronymic) и номера домашнего телефона (HomePhone).
ПClockNumber, FamilyName, Name, Patronymic, HomePhone (Librarians)
В этом примере операция проекции определяет новое отношение, которое будет содержать только атрибуты ClockNumber, FamilyNamе, Name, Patronymic и HomePhone отношения Librarians, размещенные в указанном порядке (табл. 5.2).
Таблица 5.2
Проекция отношения Librarians | ClockNumber | FamilyName | Name | Patronymic | HomePhone |
| 28 | Иванова | Алёна | Владимировна | 52-XX-75 |
| 12 | Николаенко | Любовь | Николаевна | 46-XX-19 |
| 187 | Иноземцева | Иванна | Модестовна | 775-XX-00 |
| 83 | Мальцева | Диана | Петровна | 29-XX-15 |
| 10 | Сизранцева | Татьяна | Игоревна | 370-XX-22 |
| 100 | Ставка | Лилия | Ивановна | 22-XX-01 |
| 50 | Лещенко | Алла | Федоровна | 722-XX-36 |
| 36 | Серая | Лидия | Ивановна | 254-XX-02 |
| 45 | Прохина | Томара | Львовна | 63-XX-01 |
| 78 | Самойленко | Виктория | Игоревна | 125-XX-80 |
| 69 | Степанова | Александра | Николаевна | 445-XX-65 |
| 17 | Петрова | Алина | Сергеевна | 999-XX-05 |
5.4. Операция декартового произведения
| R × S | Операция декартового произведения определяет новое отношение, которое является результатом конкатенации (сцепления) каждого кортежа отношения R с каждым кортежем отношения S. |
Операция выборки и проекции позволяют извлечь информацию только из одного отношения. Возможно возникновение и таких ситуаций, когда нужна некоторая комбинация данных из нескольких отношений. Оператор декартового произведения умножает два отношения. В результате создаётся другое отношения, где есть все возможные пары кортежей обоих отношений. Следовательно, если одно отношение имеет I кортежей и N атрибутов, а другое – J кортежей и M атрибутов, то отношение с их декартовым произведением будет содержать (I × J) кортежей и (N + M) атрибутов. Исходные отношения могут содержать атрибуты с одинаковыми именами. В таком случае одноименные атрибуты будут содержать названия отношений в виде префиксов. Это обеспечит уникальность имен атрибутов в результирующем отношении.
ПРИМЕР 5.3
Создайте список всех читателей, которые когда-либо брали книги в библиотеке, используя следующие атрибуты отношения Readers: Code, FamilyName, Name и отношения BookGiveOutRecord: Code, ReaderCode, InventoryCode.
(ПCode, FamilyName, Name (Readers)) × (ПCode, ReaderCode, InventoryCode(BookGiveOutRecord))
Результатом выполнения такой операции будет отношение, содержащее 120 кортежей и 6 атрибутов. Приводить его в полном объеме не имеет смысла. Посмотрите на его первые 12 кортежей (табл. 5.3). Первые 10 - все возможные комбинация первого кортежа отношения Readers с десятью кортежами отношения BookGiveOutRecord. Последние два приведены для того чтобы вы сравнили их значение с первыми двумя. Это первые две возможные комбинации второго кортежа отношения Readers с первыми двумя кортежами отношения BookGiveOutRecord. Следующим будет третья возможная комбинации второго кортежа отношения Readers с третьим кортежем отношения BookGiveOutRecord. И так до сто двадцатого кортежа.
Таблица 5.3
Фрагмент декартового произведения отношений Reader и BookGiveOutRecord | Readers.Code | FamilyName | Name | BookGiveOutRecord.Code | ReaderCode | InventoryCode |
| 1 | Иванов | Пётр | 1 | 2 | 6 |
| 1 | Иванов | Пётр | 2 | 3 | 4 |
| 1 | Иванов | Пётр | 3 | 6 | 3 |
| 1 | Иванов | Пётр | 4 | 4 | 6 |
| 1 | Иванов | Пётр | 5 | 7 | 7 |
| 1 | Иванов | Пётр | 6 | 9 | 12 |
| 1 | Иванов | Пётр | 7 | 11 | 10 |
| 1 | Иванов | Пётр | 8 | 7 | 8 |
| 1 | Иванов | Пётр | 9 | 9 | 12 |
| 1 | Иванов | Пётр | 10 | 12 | 15 |
| 2 | Федорец | Ирина | 1 | 2 | 6 |
| 2 | Федорец | Ирина | 2 | 3 | 4 |
В таком виде (120 кортежей) это отношение содержит больше информации, чем необходимо. Например, первый кортеж этого отношения содержит разные значения атрибутов Readers.Code и ReaderCode. Для получения искомого списка (табл. 5.4) необходимо для этого отношения произвести операцию выборки с извлечением только тех кортежей, для которых выполняется равенство Readers.Code = ReaderCode. Полностью эта операция выглядит так, как показано ниже:
σReaders.Code = ReaderCode (ПCode, FamilyName, Name(Readers)) × (ПCode, ReaderCode, InventoryCode(BookGiveOutRecord))
Таблица 5.4
Ограниченное декартово произведение отношений Reader и BookGiveOutRecord | Readers.Code | FamilyName | Name | BookGiveOutRecord.Code | ReaderCode | InventoryCode |
| 2 | Федорец | Ирина | 1 | 2 | 6 |
| 3 | Ильин | Иван | 2 | 3 | 4 |
| 6 | Носенко | Олег | 3 | 6 | 3 |
| 4 | Суренко | Дмитрий | 4 | 4 | 6 |
| 7 | Брусов | Владимир | 5 | 7 | 7 |
| 9 | Левченко | Юлия | 6 | 9 | 12 |
| 11 | Щеглов | Пётр | 7 | 11 | 10 |
| 7 | Брусов | Владимир | 8 | 7 | 8 |
| 9 | Левченко | Юлия | 9 | 9 | 12 |
| 12 | Кириленко | Виктор | 10 | 12 | 15 |
Как мы увидим далее, комбинация декартового произведения и выборки может быть сведена к одной операции - соединения.
5.5. Операция объединения
| R ∪ S | Операция объединения отношений R и S с кортежами I и J происходит в результате их конкатенации с образованием одного отношения с максимальным количеством кортежей (I + J), если кортежи-дубликаты исключены. При этом отношения R и S должны быть совместимыми по объединению. |
Объединение отношений возможно только в том случае, когда сохраняются их схемы, т.е. когда они имеют одинаковое число атрибутов с совпадающими доменами (типами данных). Такие отношения являются совместимыми по объединению. Отметим, что в некоторых случаях для получения двух совместимых по объединению отношений может быть использована операция проекции.
ПРИМЕР 5.4
Дайте список фамилии всех пользователей, занесенных в БД.
ПFamilyName(Readers) U ПFamilyName(Librarians)
Для создания совместимых по объединению отношений сначала следует применить операцию проекции, чтобы выделить из отношений Readers и Librarians столбцы с атрибутами FamilyName, исключая в случае необходимости дубликаты. Затем для комбинирования полученных промежуточных отношений следует использовать операцию объединения (табл. 5.5).
Таблица 5.5
Результат объединения отношений Readers и Librarians по атрибуту FamilyName | FamilyName |
| Брусов |
| Иванов |
| Иванова |
| Ильин |
| Иноземцева |
| Кириленко |
| Козырев |
| Коршунова |
| Левченко |
| Лещенко |
| Мальцева |
| Николаенко |
| Носенко |
| Петрова |
| Прохина |
| Самойленко |
| Светлая |
| Серая |
| Ставка |
| Степанова |
| Суренко |
| Сызранцева |
| Федорец |
| Щеглов |
| R - S | Разность двух отношений R и S состоит из кортежей, которые есть в отношении R, но отсутствуют в отношении S. Причем отношение R и S должны быть совместимыми по объединению. |
ПРИМЕР 5.5
Определите индивидуальные коды читателей, которые ни разу не брали книг в библиотеке.
ПCode(Readers)–ПReaderCode(BookGiveOutRecord)
В этом случае аналогично предыдущему примеру следует создать совместимые по объединению отношения Readers и BookGiveOutRecord, выполнив их проекцию по атрибутам Code и ReaderCode. Далее следует использовать операцию разницы (табл. 5.6).
Таблица 5.6
Разница отношений Readers и BookGiveOutRecord по атрибутам Code и ReaderCode | Code |
| 1 |
| 5 |
| 8 |
| 10 |
Как правило, пользователей интересует лишь некоторая часть всех комбинаций кортежей декартова произведения, которая удовлетворяет заданным условиям. Поэтому вместо операции декартова произведения обычно используется одна из важнейших операций реляционной алгебры - операция соединения. В результате ее выполнения на базе двух исходных отношений создается новое. Операция соединения является производной от операции декартова произведения. Она эквивалентна операции выборки из декартова произведения двух отношений только тех кортежей, которые удовлетворяют условию, что приведенная в предикате соединения. Предикат соединения является эквивалентом. Реализация операции соединения в реляционных СУБД - сверхсложный вопрос. В большинстве случаев она становится основной проблемой по повышению производительности, присущей всем реляционным системам.
Рассмотрим следующие типы соединений:
- Тета-соединение (Θ-join).
- Соединение по эквивалентности (equi-join) - отдельный вид тета-соединения.
- Естественное соединение (natural join).
- Внешнее соединение (outer join).
- Полусоединение (semi-join).
5.7.1. Операция тета-соединения
| R►◄FS | Операция тета-соединения определяет отношение, которое содержит кортежи декартового произведения отношений R и S, удовлетворяющих предикату F. Предикат F имеет вид R.aiΘS.bi, где вместо символа Θ может быть использован один из операторов сравнения (<, <=,>, >=, =, ≈). |
Операцию тета-соединение на основе базовых операций выборки и декартова произведения можно записать так:
Как и в случае с операцией декартова произведения, степенью тета-соединение называется сумма степеней операндов-отношений R и S. Если предикат F содержит только оператор равенства (=), то это - соединение по эквивалентности.
ПРИМЕР 5.6
Создайте список читателей, которые когда-либо брали книги в библиотеке (табл. 5.4).
В примере 5.3, чтобы получить этот список, используют операции декартова произведения и выборки. Однако такой же результат можно получить с помощью операции соединения по эквивалентности.
(ПCode, FamilyName, Name(Readers))►◄Readers.Code = ReaderCode(ПCode, ReaderCode, InventoryCode(BookGiveOutRecord))
5.7.2. Операция естественного соединения
| R►◄S | Соединение по эквивалентности двух отношений R и S называется естественным, если оно выполнено по всем общим атрибутам x и из результатов исключены по одному экземпляру каждого общего атрибута. |
Степенью естественного соединения является сумма степеней операндов-отношений R, S за вычитом количества общих атрибутов x. В примере с операцией тета-соединение для составления этого списка использовалась операция соединения по эквивалентности. В нем присутствовали два атрибута Readers.Code и ReaderCode, содержащие коды читателей библиотеки. Если бы они имели одинаковое имя, например ReaderCode, то для устранения одного из них можно воспользоваться операцией естественного соединения.
ПРИМЕР 5.7
Создайте список читателей, которые когда-либо брали книги в библиотеке (табл. 5.7).
(ПReaderCode, FamilyName, Name(Readers))►◄(ПCode, ReaderCode, InventoryCode(BookGiveOutRecord))
Таблица 5.7
Естественное соединения отношений Readers и BookGiveOutRecord по атрибуту ReaderCode | ReaderCode | FamilyName | Name | BookGiveOutRecord.Code | InventoryCode |
| 2 | Федорец | Ирина | 1 | 6 |
| 3 | Ильин | Иван | 2 | 4 |
| 6 | Носенко | Олег | 3 | 3 |
| 4 | Суренко | Дмитрий | 4 | 6 |
| 7 | Брусов | Владимир | 5 | 7 |
| 9 | Левченко | Юлия | 6 | 12 |
| 11 | Щеглов | Пётр | 7 | 10 |
| 7 | Брусов | Владимир | 8 | 8 |
| 9 | Левченко | Юлия | 9 | 12 |
| 12 | Кириленко | Виктор | 10 | 15 |
5.7.3. Операция внешнего соединения
Чаще всего при соединении двух отношений кортеж из одного отношения не находит соответствующего кортежа в другом отношении. Иначе говоря, в атрибутах, по которым происходит операция соединения оказываются несовпадающие значения. Может потребоваться, чтобы кортеж из одного или двух отношений был представлен в результате соединения, даже если в соответствующих атрибутах отсутствуют совпадающие значения. Эта цель может быть достигнута с помощью операции внешнего соединения.
Отсутствующие значения в результирующем отношении обозначаются определителя NULL. Преимуществом операции внешнего соединения является сохранение исходной информации: кортежи, которые теряются при использовании других типов соединений.
| R⊃◄S | Левым внешним соединением называется операция, когда кортежи отношения R, которые не имеют совпадающих значений в общих столбцах с отношением S, также включаются в результирующее отношение. |
ПРИМЕР 5.8
Определите индивидуальные коды читателей, их фамилии, имена, отчества и информацию о книгах, которые они брали в библиотеке (табл. 5.8).
(ПCode, FamilyName, Name, Patronymic(Readers))⊃◄(ПOutLibrarianCode, InventoryCode, IssueDate, ReturnDate, FactReturnDate, InLibrarianCode(BookGiveOutRecord))
Строго говоря, в примере рассмотрена операция левого (естественного) внешнего соединения, поскольку в результирующем отношении присутствуют все кортежи левого отношения. Существует также правое внешнее соединение, названное так потому, что в результирующем отношении присутствуют все кортежи правого отношения. Кроме того, существует и полное внешнее соединение, в результирующем отношении которого содержатся все кортежи обоих отношений, где для обозначения несовпадающих значений кортежей используется определитель NULL
Таблица 5.8
Левое внешнее соединение проекций отношений Readers и BookGiveOutRecord | ReaderCode | FamilyName | Name | Patronymic | OutLibrarianCode | InventoryCode | IssueDate | ReturnDate | FactReturnDate | InLibrarianCode |
| 1 | Иванов | Пётр | Иванович | NULL | NULL | NULL | NULL | NULL | NULL |
| 2 | Федорец | Ирина | Олеговна | 4 | 6 | 11.09.2004 | 25.09.2004 | 24.09.2004 | 3 |
| 3 | Ильин | Иван | Петрович | 4 | 4 | 02.09.2004 | 16.09.2004 | 11.12.2004 | 3 |
| 4 | Суренко | Дмитрий | Павлович | 3 | 6 | 30.10.2004 | 13.11.2004 | 10.01.2005 | 6 |
| 5 | Коршунова | Наталья | Юрьевна | NULL | NULL | NULL | NULL | NULL | NULL |
| 6 | Носенко | Олег | Владимирович | 4 | 3 | 02.09.2004 | 16.09.2004 | 16.09.2004 | 1 |
| 7 | Брусов | Владимир | Михайлович | 9 | 8 | 07.03.2009 | 21.03.2009 | 10.04.2009 | 10 |
| 7 | Брусов | Владимир | Михайлович | 10 | 7 | 10.11.2009 | 24.11.2009 | 24.11.2009 | 12 |
| 8 | Козирев | Алексей | Сергеевич | NULL | NULL | NULL | NULL | NULL | NULL |
| 9 | Левченко | Юлия | Павловна | 7 | 12 | 15.12.2009 | 29.12.2009 | NULL | 9 |
| 9 | Левченко | Юлия | Павловна | 8 | 12 | 05.02.2010 | 29.02.2010 | NULL | 11 |
| 10 | Светлая | Татьяна | Ивановна | NULL | NULL | NULL | NULL | NULL | NULL |
| 11 | Щеглов | Пётр | Евгеньевич | 8 | 10 | 06.02.2009 | 20.02.2009 | 19.02.2009 | 7 |
| 12 | Кириленко | Виктор | Александрович | 10 | 15 | 21.09.2010 | 05.10.2010 | 03.10.2010 | 9 |
5.7.4. Операция полусоединения
| R►FS | Операция полусоединения определяет отношение, содержащее те кортежи отношения R, которые входят в соединение отношений R и S. |
Преимущество операции полусоединения заключается в том, что она позволяет уменьшить число кортежей, которые нужно обработать для получения соединения. Это особенно важно при исчислении соединений в распределенных системах. Операцию полусоединения можно сформулировать и с помощью операторов проекции и соединения:
Здесь A - набор всех атрибутов в отношении R. На самом деле, это полутета-соединение, причем следует отметить, что существуют полусоединения по эквивалентности и полуестественные соединения.
ПРИМЕР 5.9
Создайте полный отчет, о всех читателей с именем «Дмитрий», которые когда-либо брали книги в библиотеке (табл. 5.9).
Readers►Readers.Code = BookGiveOutRecord.ReaderCode AND Reader.Name = ‘Дмитрий’BookGiveOutRecord
Таблица 5.9
Результат полусоединения отношений Readers и BookGiveOutRecord | Code | FamilyName | Name | Patronymic | ReaderCardNumber | PasportCode | Job | Post | Note |
| 4 | Суренко | Дмитрий | Павлович | 543 | 6 | НГУ, каф. геофизики | Ст. препод. | NULL |
5.8. Операция пересечения
| R ∩ S | Операция пересечения определяет отношение, содержащее кортежи, которые есть, как в отношении R, так и в отношении S. Отношение R и S должны быть совместимы по объединению. |
Операцию пересечения можно записать, используя операции разницы между отношениями: R ∩ S= R – (R – S).
ПРИМЕР 5.10
Создайте список библиотекарей, которые являются одновременно читателями. Добавить их код паспорта, фамилия, имя и отчество.
(ПPasportCode, FamilyName, Name, Patronymic(Readers)) ∩ (ПPasportCode, FamilyName, Name, Patronymic(Librarians))
Для выполнения условия совместимости отношений по объединению были выполнены соответствующие операции проекции.
Данные, которые входят в отношений «ЧИТАТЕЛИ» и «БИБЛИОТЕКОРИ» (прил. В) свидетельствуют, что результатом их пересечения является пустое множество, то есть ни один из библиотекарей не является читателем.
Операция деления может быть полезной в запросах особого типа, которые очень часто выполняются к БД. Предположим, что отношение R определенное на множестве атрибутов A, а отношение S - на множестве атрибутов B, причем B ⊆ A (т.е. B является подмножеством A). Пусть C =A - B, то есть C является множеством атрибутов отношения R, которое не являются атрибутами отношения S. Тогда определение оператора деления будет таким:
| R ÷ S | Результатом операции деления является набор кортежей отношения R, определенных на множестве атрибутов C, которое соответствует комбинациям всех кортежей отношения S. |
Операция деления эквивалентна ряду других основных операций:
T1 = ПC(R)
T2 = ПC((S × T1) – R)
T = T1 – T2
ПРИМЕР 5.11
Создайте список имён, фамилий, отчеств и кодов паспортов читателей, родившихся после 1 декабря 1960 года.
R = ПCode, PassportCode, FamilyName, Name, Patronymic(Readers) (табл. 5.10);
S = ПCode(σBirthday > 31.12.1960(PasportData)) (табл. 5.11);
R ÷ S = (ПCode, PassportCode, FamilyName, Name, Patronymic(Readers)) ÷ (ПCode(σBirthday > 31.12.1960(PasportData))) (табл. 5.12).
Для решения поставленной задачи сначала необходимо получить отношение R. Для этого выполнена проекция отношения Readers (табл. 5.10). Затем определить отношение S. Для этого получена проекцию отношении PasportData. В нём с помощью оператора выборки найдены все коды паспортов с датой рождения после 31 декабря 1960 года (табл. 5.11). Теперь получим результат деления отношения R на S (табл. 5.12).
Таблица 5.10
Отношение R | Code | PasportCode | FamilyName | Name | Patronymic |
| 1 | 4 | Иванов | Петр | Иванович |
| 2 | 1 | Федорец | Ирина | Олеговна |
| 3 | 11 | Ильин | Иван | Петрович |
| 4 | 6 | Суренко | Дмитрий | Павлович |
| 5 | 8 | Коршунова | Наталья | Юрьевна |
| 6 | 5 | Носенко | Олег | Владимирович |
| 7 | 24 | Брусов | Владимир | Михайлович |
| 8 | 15 | Козырев | Алексей | Сергеевич |
| 9 | 18 | Левченко | Юлия | Павловна |
| 10 | 22 | Светлая | Татьяна | Ивановна |
| 11 | 14 | Щеглов | Петр | Евгеньевич |
| 12 | 17 | Кириленко | Виктор | Александрович |
Таблица 5.11
Отношение S | Code |
| 3 |
| 5 |
| 7 |
| 8 |
| 12 |
| 14 |
| 15 |
| 16 |
| 18 |
| 19 |
| 20 |
| 21 |
| 22 |
| 23 |
| 24 |
Таблица 5.12
Результат R ÷ S | PasportCode | FamilyName | Name | Patronymic |
| 8 | Коршунова | Наталья | Юрьевна |
| 5 | Носенко | Олег | Владимирович |
| 24 | Брусов | Владимир | Михайлович |
| 15 | Козырев | Алексей | Сергеевич |
| 18 | Левченко | Юлия | Павловна |
| 22 | Светлая | Татьяна | Ивановна |
| 14 | Щеглов | Петр | Евгеньевич |
5.10. КОНТРОЛЬНЫЕ ВОПРОСЫ
- Какие особенности и свойства реляционной алгебры Вам известны
- Какие операции реляционной алгебры Вы знаете?
- Какая существует разница между операциями выборки и проекции?
- В каком из двух отношений количество атрибутов и кортежей будет больше, если первое является результатом операции декартова произведения отношений R с I кортежей и N атрибутов и S с J кортежей и M атрибутов, а второе - результатом операции объединения тех же отношений?
- В чем заключается сущность операций реляционной алгебры, которые требуют совместных с объединением исходных отношений?
- Какие операции реляционной алгебры являются производными от операции декартова произведения?
- Какой из операторов сравнения превращает Θ-соединения в натуральное?
- В чем разница между внешним и другими типами соединений?
- Как формируется отношение, которое является результатом работы известных Вам типов внешних соединений?
Вывод
Синтаксис SQL-операторов, которые используются для обработки данных в реляционных СУБД разных разработчиков, может отличаться, но операции реляционной алгебры является математическим фундаментом, который их объединяет. В случае необходимости этот факт может быть полезным для конвертации БД с реляционной СУБД, которая используется для решения текущей задачи организации, в формат реляционной СУБД другого разработчика.